Elementer av kombinatorikk. Hells hemmeligheter eller en steg-for-steg algoritme for å vinne i lotto 5 av 25 hvor mange kombinasjoner

Hallo!

Jeg heter Ivan Melnikov! Jeg er utdannet ved National Technical University "KhPI", Fakultet for ingeniørvitenskap og fysikk, spesialitet "Anvendt matematikk", en lykkelig familiemann og bare en fan av sjansespill. Siden barndommen har jeg vært interessert i lotterier. Jeg har alltid lurt på hvilke lover enkelte baller faller ut. Siden jeg var 10 år gammel har jeg spilt inn lotteriresultater og deretter analysert dataene.

Vennlig hilsen,

Ivan Melnikov.

1. Matematiske odds for å vinne

   • Enkel utregning med faktorialer

De vanligste lotteriene i verden er lykkespill som "5 av 36" og "6 av 45". La oss beregne sjansen for å vinne i lotto ved hjelp av sannsynlighetsteori.

Et eksempel på beregning av muligheten for å motta en jackpot i "5 av 36"-lotteriet:

Det er nødvendig å dele antall ledige celler med antall mulige kombinasjoner. Det vil si at det første sifferet kan velges fra 36, ​​det andre fra 35, det tredje fra 34, og så videre.

Derfor er her formelen:

Antall mulige kombinasjoner i et "5 av 36"-lotteri = (36*35*34*33*32) / (1*2*3*4*5) = 376.992

Sjansen for å vinne er 1 av nesten 400 000.

La oss gjøre det samme for et lotteri som 6 av 45.

Antall mulige kombinasjoner = “6 av 45” = (45*44*43*42*41*40) / (1*2*3*4*5*6) = 9.774.072.

Følgelig er sjansen for å vinne nesten 1 av 10 millioner.

• Litt om sannsynlighetsteori

I følge en lenge kjent teori har hver ball i hvert påfølgende søk en absolutt lik sjanse for å falle ut sammenlignet med de andre.

Men ikke alt er så enkelt, selv ikke etter sannsynlighetsteori. La oss se nærmere på eksemplet med å kaste en mynt. Første gang vi fikk hoder, så neste gang er sannsynligheten for å få haler mye høyere. Hvis hoder kommer opp igjen, så forventer vi haler neste gang med enda større sannsynlighet.

Med ballene som kommer ut av lotteriautomatene, handler det om den samme historien, men litt mer komplisert og med et mer betydelig antall variabler. Hvis en ball trekkes 3 ganger og den andre trekkes 10 ganger, vil sannsynligheten for at den første ballen trekkes være høyere enn for den andre. Det er verdt å merke seg at denne loven blir flittig brutt av arrangørene av noen lotterier, som skifter lotterimaskiner fra tid til annen. En ny sekvens vises i hver nye lottoautomat.

Noen arrangører bruker også en egen loddautomat for hver ball. Dermed er det nødvendig å beregne sannsynligheten for at hver ball faller ut i hver enkelt lottomaskin. På den ene siden gjør dette oppgaven litt lettere, på den andre siden kompliserer det den.

Men dette er bare en sannsynlighetsteori, som, som det viser seg, egentlig ikke fungerer. La oss se hvilke hemmeligheter det er, basert på tørr vitenskap og statistiske data akkumulert over flere tiår.

1. Hvorfor fungerer ikke sannsynlighetsteori?

   • Mindre enn ideelle forhold

Det første som er verdt å snakke om er kalibreringen av lotterimaskiner. Ingen av lotteriautomatene er perfekt kalibrert.

Det andre forbeholdet er at diameteren på lotterikuler heller ikke er den samme. Selv forskjeller på den minste brøkdel av millimeter spiller en rolle i frekvensen av en bestemt ball som faller ut.

Den tredje detaljen er den forskjellige vekten på ballene. Igjen, forskjellen virker kanskje ikke signifikant i det hele tatt, men den påvirker også statistikken, og betydelig.

• Summen av vinnende tall

Hvis vi ser på statistikken over vinnende tall i et "6 av 45" lotteri, vil vi legge merke til et interessant faktum: summen av tallene som spillere satser på varierer mellom 126 og 167.

Summen av de vinnende lottotallene for "5 av 36" er en litt annen historie. Her blir vinnertallene 83-106.

• Jevn eller ujevn?

Hvilke tall tror du finnes oftest på vinnerlodd? Til og med? Merkelig? Jeg kan fortelle deg med full tillit at i "6 av 45" lotterier er disse tallene likt delt.

Men hva med "5 av 36"? Tross alt må du bare velge 5 baller; det kan ikke være like mange partall og oddetall. Så her er det. Etter å ha analysert resultatene av lotterier av denne typen de siste fire tiårene, kan jeg si at litt, men fortsatt oftere, oddetall vises i vinnende kombinasjoner. Spesielt de som inneholder tallet 6 eller 9. For eksempel 19, 29, 39, 69 og så videre.

• Populære grupper av tall

For et lotteri av typen "6 til 45" deler vi betinget tallene inn i 2 grupper - fra 1 til 22 og fra 23 til 45. Det skal bemerkes at i vinnende lodd er forholdet mellom tallene som tilhører gruppen 2 til 4. Det vil si at enten vil billetten inneholde 2 tall fra gruppen fra 1 til 22 og 4 tall fra gruppen fra 23 til 45 eller omvendt (4 tall fra den første gruppen og 2 fra den andre).

Jeg kom til en lignende konklusjon da jeg analyserte statistikken til lotterier som "5 av 36". Bare i dette tilfellet er gruppene delt opp litt annerledes. La oss utpeke den første gruppen som inkluderer tallene fra 1 til 17, og den andre den som inneholder de resterende tallene fra 18 til 35. Forholdet mellom tallene fra den første gruppen til den andre i vinnende kombinasjoner i 48 % av tilfellene er 3 til 2, og i 52 % av tilfellene – tvert imot, 2 til 3.

• Er det verdt å satse på tall fra tidligere trekninger?

Det er bevist at i 86 % av tilfellene gjentar en ny tegning et tall som allerede har dukket opp i tidligere tegninger. Derfor trenger du bare å følge trekningene til lotteriet du er interessert i.

• Påfølgende tall. Å velge eller ikke velge?

Sjansen for at 3 påfølgende tall vises på en gang er svært lav, mindre enn 0,09 %. Og hvis du vil satse på 5 eller 6 påfølgende tall på en gang, er det praktisk talt ingen sjanse. Velg derfor forskjellige tall.

• Tall med ett enkelt trinn: vinn eller tap?

Du bør ikke satse på tall som vises i samme rekkefølge. For eksempel trenger du definitivt ikke velge trinn 2 og plassere et spill med dette trinnet. 10, 13, 16, 19, 22 er definitivt en tapende kombinasjon.

• Mer enn én billett: ja eller nei?

Det er bedre å spille en gang hver 10. uke med 10 billetter enn en gang i uken med en. Og også spille i grupper. Du kan vinne en stor pengepremie og dele den mellom flere personer.

1. Verdens lotteristatistikk

   • Mega millioner

Et av de mest populære lotteriene i verden ble utført i henhold til følgende prinsipp: du må velge 5 tall av 56, samt 1 av 46 for den såkalte gullkulen.

For 5 matchede baller og 1 korrekt navngitt gullball, mottar den heldige vinneren jackpotten.

De gjenværende avhengighetene er vist i tabellen:

Statistikk over tapte vanlige baller for hele varigheten av de ovennevnte lotteritrekningene.

Statistikk over gullkuler trukket gjennom Mega Millions-tegningene.

De hyppigst trukket kombinasjonene i lotteriet er vist i tabellen nedenfor:

• Powerball-lotteri hvor mer enn et dusin heldige mennesker har klart å vinne jackpotten. Du må velge 7 hovedspillnumre og to Powerballs.

1. Vinnernes historier

   • Heldige landsmenn

Evgeny Sidorov fra Moskva fikk 35 millioner i 2009, før det fikk Nadezhda Mekhametzyanova fra Ufa jackpoten på 30 millioner. "Russian Lotto" sendte ytterligere 29,5 millioner til Omsk til vinneren, som ikke ønsket å identifisere seg. Generelt er det å vinne jackpotter en god vane for russere

• 390 millioner amerikanske dollar i én hånd

I lotteriet vi allerede snakket om, vant Mega Millions, en heldig vinner som ønsket å være anonym $390 millioner. Og dette er langt fra et sjeldent tilfelle. I det samme lotteriet i 2011 klarte to personer å treffe jackpotten, som på det tidspunktet besto av et beløp på 380 millioner. Pengepremien ble delt i to deler og delt ut til personer som gjettet vinnertallene.

En pensjonist fra South Carolina bestemte seg for å delta i Powerball-lotteriet og vant 260 millioner, som han bestemte seg for å bruke på utdanningen til barna sine, og kjøpte også et hus, flere biler til familien, og reiste deretter.

1. konklusjoner

Så her er en oppsummering av de mest effektive reglene, som du er sikker på å vinne:

1. Summen av alle tallene du satser på på et lodd må beregnes ved å bruke følgende formel:

Mengde = ((1 + n)/2)*z + 2 +/- 12 %

n – maksimalt innsatsnummer, for eksempel 36 i et "5 av 36"-lotteri

z – antall baller du satser på, for eksempel 5 for "5 av 36"-lotteriet

Det vil si at for "5 av 36" vil beløpet være slik:

((1+36)/2)*5 + 2 +/-12% = 18,5*5+2 +/-12% = 94,5 +/-12%

I dette tilfellet, fra 94,5 + 12% til 94,5 - 12%, det vil si fra 83 til 106.

1. Sats likt på partall og oddetall.
2. Del alle tallene i to store grupper i to. Forholdet mellom antall tall på en vinnende lodd er 1 til 2 eller 2 til 1.
3. Følg statistikken og spill på tallene som kom ut i tidligere trekninger.
4. Ikke sats på tall med ett trinn.
5. Det er bedre å spille sjeldnere, men kjøpe flere billetter på en gang, og også komme sammen med venner og slektninger.

Generelt, vær modig! Følg mine regler, plasser spill, analyser statistikk og vinn!

Kombinatorikk er en gren av matematikken som studerer spørsmål om hvor mange forskjellige kombinasjoner, under visse betingelser, kan lages av gitte objekter. Det grunnleggende om kombinatorikk er svært viktig for å estimere sannsynlighetene for tilfeldige hendelser, fordi Det er de som lar oss beregne det grunnleggende mulige antallet forskjellige scenarier for utvikling av hendelser.

Grunnformel for kombinatorikk

La det være k grupper av elementer, og den i-te gruppen består av n i elementer. La oss velge ett element fra hver gruppe. Da bestemmes det totale antallet N måter et slikt valg kan gjøres på av forholdet N=n 1 *n 2 *n 3 *...*n k .

Eksempel 1. La oss forklare denne regelen med et enkelt eksempel. La det være to grupper av elementer, og den første gruppen består av n 1 elementer, og den andre - av n 2 elementer. Hvor mange forskjellige elementpar kan lages fra disse to gruppene, slik at paret inneholder ett element fra hver gruppe? La oss si at vi tok det første elementet fra den første gruppen og, uten å endre det, gikk gjennom alle mulige par, og endret bare elementene fra den andre gruppen. Det kan være n 2 slike par for dette elementet. Så tar vi det andre elementet fra den første gruppen og lager også alle mulige par for det. Det vil også være n 2 slike par. Siden det bare er n 1 elementer i den første gruppen, vil totalt mulige alternativer være n 1 *n 2.

Eksempel 2. Hvor mange tresifrede partall kan lages fra sifrene 0, 1, 2, 3, 4, 5, 6, hvis sifrene kan gjentas?
Løsning: n 1 =6 (fordi du kan ta et hvilket som helst tall fra 1, 2, 3, 4, 5, 6 som det første sifferet), n 2 =7 (fordi du kan ta et hvilket som helst tall fra 0 som det andre sifferet , 1, 2 , 3, 4, 5, 6), n 3 =4 (siden et hvilket som helst tall fra 0, 2, 4, 6 kan tas som det tredje sifferet).
Så, N=n 1 *n 2 *n 3 =6*7*4=168.

I tilfellet når alle grupper består av like mange elementer, dvs. n 1 =n 2 =...n k =n vi kan anta at hvert utvalg er gjort fra samme gruppe, og elementet etter seleksjon returneres til gruppen. Da er antallet på alle utvalgsmetodene n k . Denne metoden for seleksjon i kombinatorikk kalles prøver med retur.

Eksempel 3. Hvor mange firesifrede tall kan lages av sifrene 1, 5, 6, 7, 8?
Løsning. For hvert siffer i et firesifret tall er det fem muligheter, som betyr N=5*5*5*5=5 4 =625.

Tenk på et sett som består av n elementer. I kombinatorikk kalles dette settet generell befolkning.

Antall plasseringer av n elementer med m

Definisjon 1. Overnatting fra n elementer av m i kombinatorikk evt bestilt sett fra m ulike elementer valgt fra befolkningen i n elementer.

Eksempel 4. Ulike arrangementer av tre elementer (1, 2, 3) med to vil være settene (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3) , 2). Plasseringer kan avvike fra hverandre både i elementer og rekkefølge.

Antall plasseringer i kombinatorikk er angitt med A n m og beregnes med formelen:

Kommentar: n!=1*2*3*...*n (les: «en factorial»), i tillegg antas det at 0!=1.

Eksempel 5. Hvor mange tosifrede tall er det der titallet og enhetssifferet er forskjellige og odde?
Løsning: fordi Hvis det er fem oddetall, nemlig 1, 3, 5, 7, 9, så kommer denne oppgaven ned på å velge og plassere to av de fem forskjellige sifrene i to forskjellige posisjoner, dvs. de angitte tallene vil være:

Definisjon 2. Kombinasjon fra n elementer av m i kombinatorikk evt uordnet sett fra m ulike elementer valgt fra befolkningen i n elementer.

Eksempel 6. For settet (1, 2, 3) er kombinasjonene (1, 2), (1, 3), (2, 3).

Antall kombinasjoner av n elementer, m hver

Antall kombinasjoner er angitt med C n m og beregnes med formelen:

Eksempel 7. På hvor mange måter kan en leser velge to bøker av seks tilgjengelige?

Løsning: Antall metoder er lik antall kombinasjoner av seks bøker av to, dvs. er lik:

Permutasjoner av n elementer

Definisjon 3. Permutasjon fra n elementer kalles noen bestilt sett disse elementene.

Eksempel 7a. Alle mulige permutasjoner av et sett som består av tre elementer (1, 2, 3) er: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3) , (3, 2, 1), (3, 1, 2).

Antall forskjellige permutasjoner av n elementer er betegnet med P n og beregnes med formelen P n =n!.

Eksempel 8. På hvor mange måter kan syv bøker av forskjellige forfattere ordnes på én rad i en hylle?

Løsning: Dette problemet handler om antall permutasjoner av syv forskjellige bøker. Det er P 7 =7!=1*2*3*4*5*6*7=5040 måter å ordne bøkene på.

Diskusjon. Vi ser at antall mulige kombinasjoner kan beregnes i henhold til forskjellige regler (permutasjoner, kombinasjoner, plasseringer) og resultatet vil bli annerledes, fordi Beregningsprinsippet og selve formlene er forskjellige. Ser du nøye på definisjonene, vil du legge merke til at resultatet avhenger av flere faktorer samtidig.

For det første, fra hvor mange elementer vi kan kombinere settene deres (hvor stor er totalen av elementer).

For det andre avhenger resultatet av størrelsen på settene med elementer vi trenger.

Til slutt er det viktig å vite om rekkefølgen av elementene i settet er viktig for oss. La oss forklare den siste faktoren ved å bruke følgende eksempel.

Eksempel 9. Det er 20 personer tilstede på foreldremøtet. Hvor mange ulike alternativer er det for sammensetningen av foreldreutvalget dersom det skal omfatte 5 personer?
Løsning: I dette eksemplet er vi ikke interessert i rekkefølgen av navn på komitélisten. Hvis, som et resultat, de samme menneskene viser seg å være en del av det, så er dette i betydning for oss det samme alternativet. Derfor kan vi bruke formelen til å beregne tallet kombinasjoner med 20 elementer 5 hver.

Ting vil være annerledes hvis hvert komitémedlem i utgangspunktet er ansvarlig for et spesifikt arbeidsområde. Da er det med samme listesammensetning av komiteen muligens 5 inni den! alternativer kombinasjonsmuligheter den saken. Antall forskjellige (både i sammensetning og ansvarsområde) alternativer bestemmes i dette tilfellet av antallet plasseringer med 20 elementer 5 hver.

Selvtestoppgaver
1. Hvor mange tresifrede partall kan lages fra sifrene 0, 1, 2, 3, 4, 5, 6, hvis sifrene kan gjentas?

2. Hvor mange femsifrede tall er det som leses likt fra venstre til høyre og fra høyre til venstre?

3. Det er ti fag i klassen og fem leksjoner om dagen. På hvor mange måter kan du lage en tidsplan for én dag?

4. På hvor mange måter kan 4 delegater velges ut til en konferanse hvis det er 20 personer i gruppen?

5. På hvor mange måter kan åtte forskjellige bokstaver legges i åtte forskjellige konvolutter, hvis bare én bokstav legges i hver konvolutt?

6. En kommisjon bestående av to matematikere og seks økonomer bør være sammensatt av tre matematikere og ti økonomer. På hvor mange måter kan dette gjøres?

La oss telle i MS EXCEL antall kombinasjoner av n elementer med k. Ved hjelp av formler vil vi vise på arket alle variantene av kombinasjoner (engelsk oversettelse av begrepet: Kombinasjoner uten repetisjon).

Kombinasjoner av n forskjellige elementer av k elementer er kombinasjoner som er forskjellige i minst ett element. Nedenfor er for eksempel ALLE 3-elementkombinasjoner hentet fra et sett bestående av 5 elementer (1; 2; 3; 4; 5):

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Merk: Dette er en artikkel om å telle antall kombinasjoner med MS EXCEL. Vi anbefaler å lese det teoretiske grunnlaget i en spesialisert lærebok. Å lære kombinasjoner fra denne artikkelen er en dårlig idé.

Forskjellen mellom kombinasjoner og plasseringer

Viser alle kombinasjoner av kombinasjoner

I eksempelfilen lages formler for å vise alle kombinasjoner for gitte n og k.

Ved å spesifisere antall elementer i settet (n) og antall elementer som vi velger fra det (k), ved å bruke formler kan vi vise alle kombinasjoner.

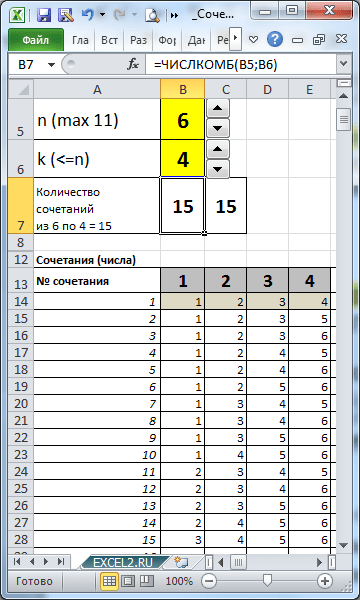
Oppgave

En biltransporter kan frakte 4 biler. Det er nødvendig å transportere 7 forskjellige biler (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). På hvor mange forskjellige måter kan den første biltransportøren fylles? Den spesifikke plasseringen av bilen i biltransporteren er ikke viktig.

Vi må bestemme antallet Kombinasjoner 7 biler på 4 plasser av en biltransporter. De. n=7 og k=4. Det viser seg at det er 35 slike alternativer =NUMCOMB(7,4).

La oss tilfeldig sammenligne numeriske verdier med bilmerker og lage forkortelser for merkenavn: LADA Granta (LG=1), Hyundai Solaris (HS=2), ...

Uheldige kombinasjoner 5/2 og 5/9

Disse kombinasjonene, som inkluderer Frightful Five, er så åpenbart uheldige at hver feng shui-lærebok uten unntak advarer om dem.

Faktisk bør en feng shui-profesjonell ikke lenger stoppe ved hvordan man identifiserer og nøytraliserer disse kombinasjonene. Det antas at hver fan av Flying Star feng shui allerede vet nok om farene som er skjult i 2/5 eller 5/2 kombinasjoner. De bringer ulykke, tap og svikt til hjemmet, uavhengig av rekkefølgen de kombineres i. Med denne kombinasjonen er alt veldig klart - 5 og 2 er alltid dårlige, både i inneværende og i neste periode. Forhåpentligvis har du allerede hatt en god følelse for det, så vær forsiktig.

Kombinasjonen av 2 og 5 blir gjenstand for profesjonell feng shui-betraktning bare når den ikke kan håndteres med vanlige midler. Hvis du oppdager at beskyttelsesmidlene dine ikke fungerer og kombinasjonen av 5 og 2 allerede begynner å manifestere seg i form av ulykker, alvorlige sykdommer, økonomiske vanskeligheter og andre problemer - så tilbyr Feng Shui flere måter å bekjempe det.

I normale tilfeller er det nok å henge en seksrørs "syngende vind" for å gi kontroll over 5/2. Jo sterkere denne kombinasjonen - for eksempel hvis den støttes av årlige eller månedlige 5/2 stjerner - jo større bør den "syngende vinden" være. Hvis dette ikke er nok, må du gjøre følgende: ta seks store metallmynter (med firkantede hull i midten), tre en tråd gjennom dem og heng dem fra taket. Hvis den uheldige kombinasjonen er i frontpalasset, heng seks mynter over inngangsdøren. Legg deretter en annen haug med seks mynter på gulvet og dekk den med teppet. Den metalliske yin-energien i disse myntene vil holde 5/2 under kontroll.

Den neste måten er å sette opp et fellerom i palasset der 5/2 ligger. Sørg for at døren til dette rommet er lukket. Du trenger bare å ventilere dette rommet fra tid til annen, og dermed frigjøre den akkumulerte negative energien.

Bildet viser et hus fra den syvende perioden. Her ligger 5/9 og 9/5 i vest og sørvest, noe som setter hovedsoverommet i fare. For å holde 5/9 under kontroll, plasser et blått teppe på soverommet og en stor kobbervase. 9/5-kombinasjonen på badet er ganske undertrykt av toalettet. Når det gjelder kombinasjonene 5/9 og 9/5, bør det tas i betraktning at de under noen omstendigheter kan bety enda større fare. Hvis 2 legger sykdom til 5, så styrker 9 den onde 5. Dette skyldes det faktum at 9 er ild, som føder jorden. I tillegg har ni generelt egenskapen til å multiplisere og øke alt. Hun gjør gode stjerner enda bedre, men hun gjør uheldige til dødelige! For å kontrollere 9/5, plasser en kobbervase med vann* (men ikke på soverommet). Her vil metall undertrykke 5, og vann vil slukke brann. Det anbefales ikke å holde vann på soverommet i stedet, det er bedre å bruke blå farge. Metall i dette tilfellet vil være veldig nyttig, siden dets svekkelseseffekt er 5 ganger sterkere enn effekten av vann. på veggen.

Kombinasjoner av Ho-tu tall 1 og 6. Elementet i denne kombinasjonen er vann, den opprinnelige retningen er nord, men denne kombinasjonen betegner god jordisk qi, som bringer lykke og lykke til.

Uansett hvor hun er, bør hennes fordelaktige jordiske qi aktiveres ved hjelp av jordiske gjenstander - steiner, steinblokker eller krystall. Dersom det er fjell i retningen der Ho-tu 6/1 ligger, fungerer dette som en aktiverende faktor.

Det er en annen tilnærming til å tolke Ho-tu-tall, men denne gangen inkluderer kombinasjonene deres enten periodestjerner og fjell-/vannstjerner, eller fjell- og vannstjerner. Med denne tilnærmingen endres betydningen av Ho-tu-tall avhengig av hvilken periode de tilhører. Hvis de tilhører en økende periode, anses kombinasjonen deres som heldig, og hvis de tilhører en avtagende periode, anses den som uheldig. Hvis perioden er avtagende, eller ødeleggende, medfører Ho-tu-tall stor fare. Husk at tolkningene av tallene som er gitt her, er riktige bare hvis de er plassert i sektoren av inngangsdøren til huset. I ethvert annet palass mister de sin mening.

I perioden med økning:

4 og 9 bringer lykke til i virksomheten. Rikdom er ervervet ærlig.

4 og 9 er i økende periode i nord. De beste mulighetene er i de vestlige og nordvestlige palassene.

Poenget er at... basiskart over den åttende perioden med 8 i sentrum, tallet 5 flyr til det sørvestlige palasset. Det bør huskes at tallet 5 ikke har sin egen yin- eller yang-flyordre. Hver gang 5 flyr til et nytt palass, tar hun på seg flyrekkefølgen til det palasset. Dermed kan 5 ha enten en yin (minus) eller en yang (pluss) flytur; avhengig av palasset hun okkuperer. Men i den åttende perioden fløy tallet 5 mot sørvest, hvor det i den opprinnelige Yao-shu-plassen er en stjerne 2, det vil si et partall. Derfor, i den åttende perioden, flyr stjerne 5 yin, yang, yang eller minus, pluss, pluss. I tillegg vil selve tallet 7, som i sin natur regnes som en aggressiv stjerne av kriger og vold, bli til en uheldig stjerne i den 8. perioden. Du må definitivt huske dette og passe deg for dens farlige påvirkning. Innbyggerne måtte tenke fremover på hvordan de kunne få mest mulig ut av stjerneplasseringene på det åttende periodediagrammet. Hvis døren i åttende periode er plassert på C1, vil vi få et frontpalass med en kombinasjon av fjell/vann i form av en dobbel åtte, og dette er et tegn på ekte flaks.

På kartet over huset ditt fra den åttende perioden med frontretningen C1, er den doble 8-en i det fremre palasset. Dette er en av de mest vellykkede kombinasjonene. Derfor, for å realisere de gunstige mulighetene for dobbel 8, bør feng shui-beskyttelsesprodukter brukes på Efim og Annas soverom. I Efims antatte soverom er det svært dårlige tall 9, 5 og 7, som varsler vold, tap og sykdom. For å holde 9/7-kombinasjonen under kontroll, må Efims soverom dekoreres i blåtoner, som symboliserer yin-vann. Bare ikke bruk ekte vann under noen omstendigheter! Det blå soverommet vil undertrykke fjellstjernen 9 og svekke vannstjernen 7.